Many experimental works have observed that generalization in deep RL appears to be difficult: although RL agents can learn to perform very complex tasks, they don't seem to generalize over diverse task distributions as well as the excellent generalization of supervised deep nets might lead us to expect. In this blog post, we will aim to explain why generalization in RL is fundamentally harder, and indeed more difficult even in theory.
We will show that attempting to generalize in RL induces implicit partial observability, even when the RL problem we are trying to solve is a standard fully-observed MDP. This induced partial observability can significantly complicate the types of policies needed to generalize well, potentially requiring counterintuitive strategies like information-gathering actions, recurrent non-Markovian behavior, or randomized strategies. Ordinarily, this is not necessary in fully observed MDPs but surprisingly becomes necessary when we consider generalization from a finite training set in a fully observed MDP. This blog post will walk through why partial observability can implicitly arise, what it means for the generalization performance of RL algorithms, and how methods can account for partial observability to generalize well.
Learning By Example¶
Before formally analyzing generalization in RL, let’s begin by walking through two examples that illustrate what can make generalizing well in RL problems difficult.
The Image Guessing Game: In this game, an RL agent is shown an image each episode, and must guess its label as quickly as possible (Figure 1). Each timestep, the agent makes a guess; if the agent is correct, then the episode ends, but if incorrect, the agent receives a negative reward, and must make another guess for the same image at the next timestep. Since each image has a unique label (that is, there is some “true” labelling function $f_{true}: x \mapsto y$) and the agent receives the image as observation, this is a fully-observable RL environment.
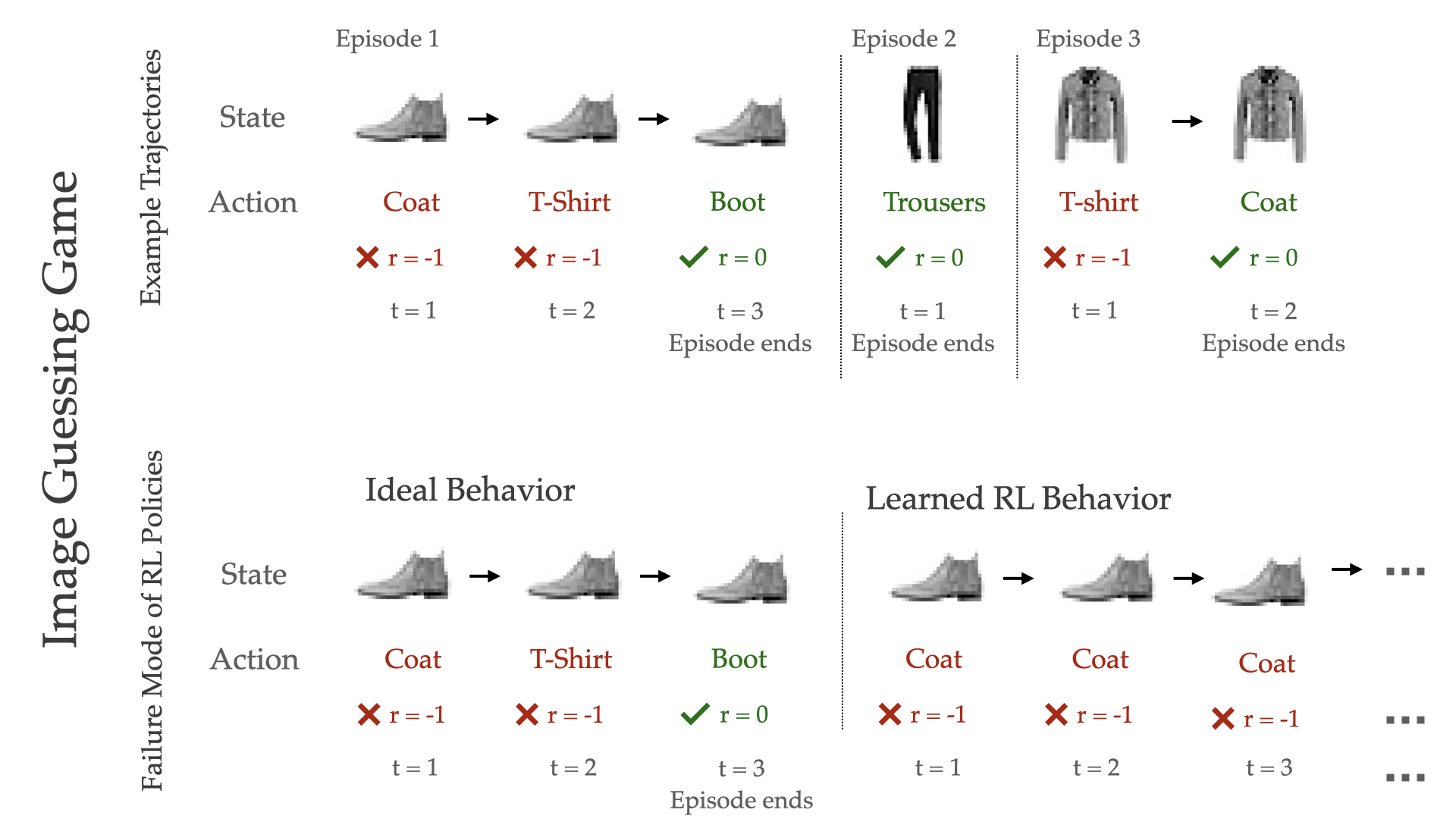
Suppose we had access to an infinite number of training images, and learned a policy using a standard RL algorithm. This policy will learn to deterministically predict the true label ($y := f_{true}(x)$), since this is the highest return strategy in the MDP (as a sanity check, recall that the optimal policy in an MDP is deterministic and memoryless). If we only have a limited set of training images, an RL algorithm will still learn the same strategy, deterministically predicting the label it believes matches the image. But, does this policy generalize well? On an unseen test image, if the agent’s predicted label is correct, the highest possible reward is attained; if incorrect, the agent receives catastrophically low return, since it never guesses the correct label. This catastrophic failure mode is ever-present, since even though modern deep nets improve generalization and reduce the chance of misclassification, error on the test set cannot be completely reduced to 0.
Can we do better than this deterministic prediction strategy? Yes, since the learned RL strategy ignores two salient features of the guessing game: 1) the agent receives feedback through an episode as to whether its guesses are correct, and 2) the agent can change its guess in future timesteps. One strategy that better takes advantage of these features is process-of-elimination; first, selecting the label it considers most likely, and if incorrect, eliminating it and adapting to the next most-likely label, and so on. This type of adaptive memory-based strategy, however, can never be learned by a standard RL algorithm like Q-learning, since they optimize MDP objectives and only learn deterministic and memoryless policies.
Maze-Solving: A staple of RL generalization benchmarks, the maze-solving problem requires an agent to navigate to a goal in a maze given a birds-eye view of the whole maze. This task is fully-observed, since the agent’s observation shows the whole maze. As a result, the optimal policy is memoryless and deterministic: taking the action that moves the agent along the shortest path to the goal. Just as in the image-guessing game, by maximizing return within the training maze layouts, an RL algorithm will learn policies akin to this “optimal” strategy -- at any state, deterministically taking the action that it considers most likely to be on the shortest path to the goal.
This RL policy generalizes poorly, since if the learned policy ever chooses an incorrect action, like running into a wall or doubling back on its old path, it will continue to loop the same mistake and never solve the maze. This failure mode is completely avoidable, since even when the RL agent initially takes such an “incorrect” action, after attempting to follow it, the agent receives information (e.g. the next observation) as to whether or not this was a good action. To generalize as well as possible, an agent should adapt its chosen actions if the original actions led to unexpected outcomes , but this behavior eludes standard RL objectives.
What’s Going On? RL and Epistemic Uncertainty¶
In both the guessing game and the maze task, the gap between behavior learned by standard RL algorithms and by policies that actually generalize well, seemed to arise when the agent incorrectly (or could not) identified how the dynamics of the world behave. Let’s dig deeper into this phenomenon.
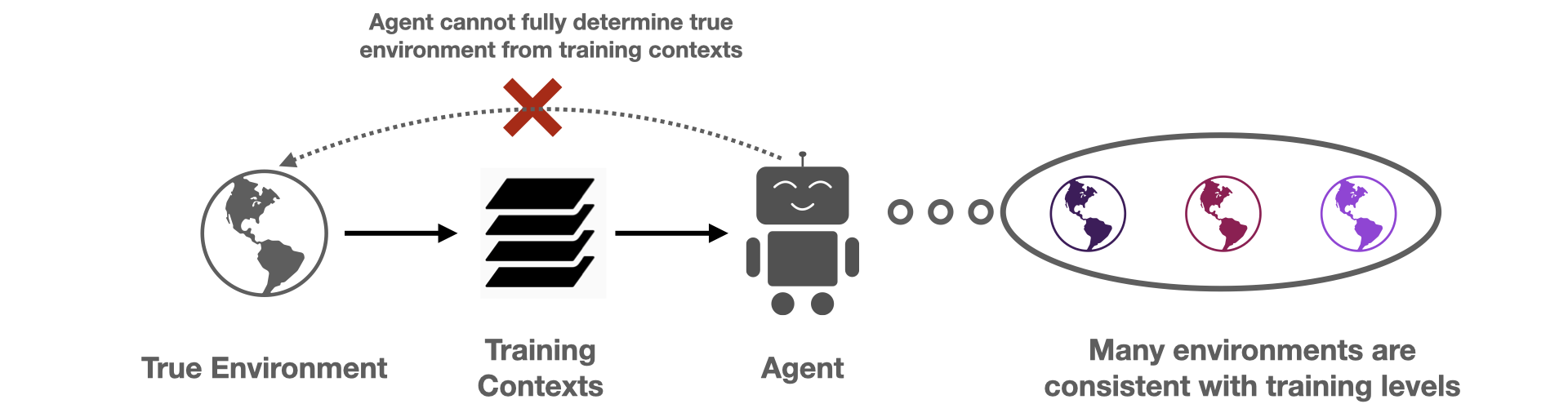
When the agent is given a small training set of contexts, there are many dynamics models that match the provided training contexts, but differ on held-out contexts. These conflicting hypotheses epitomize the agent’s epistemic uncertainty from the limited training set. While uncertainty is not specific to RL, how it can be handled in RL is unique due to the sequential decision making loop. For example, the agent can actively regulate how much epistemic uncertainty it is exposed to, for example by choosing a policy that only visits states where the agent is highly confident about the dynamics. Even more importantly, the agent can change its epistemic uncertainty at evaluation time by accounting for the information that it receives through the trajectory. Suppose for an image in the guessing game, the agent is initially uncertain between the t-shirt / coat labels. If the agent guesses “t-shirt” and receives feedback that this was incorrect, the agent changes its uncertainty and becomes more confident about the “coat” label, meaning it should consequently adapt and guess "coat" instead.
Epistemic POMDPs and Implicit Partial Observability¶
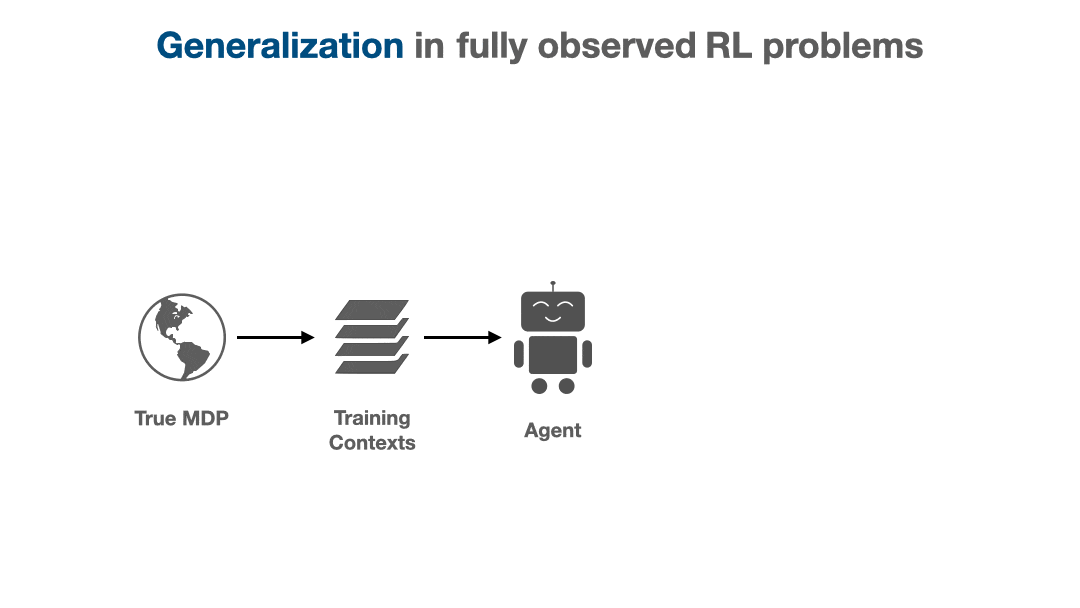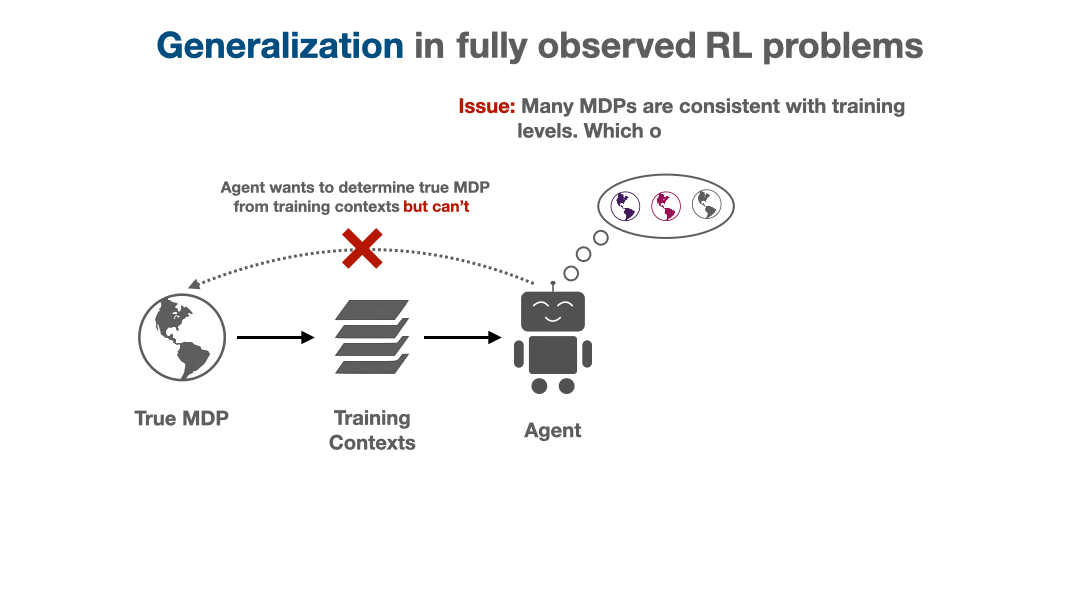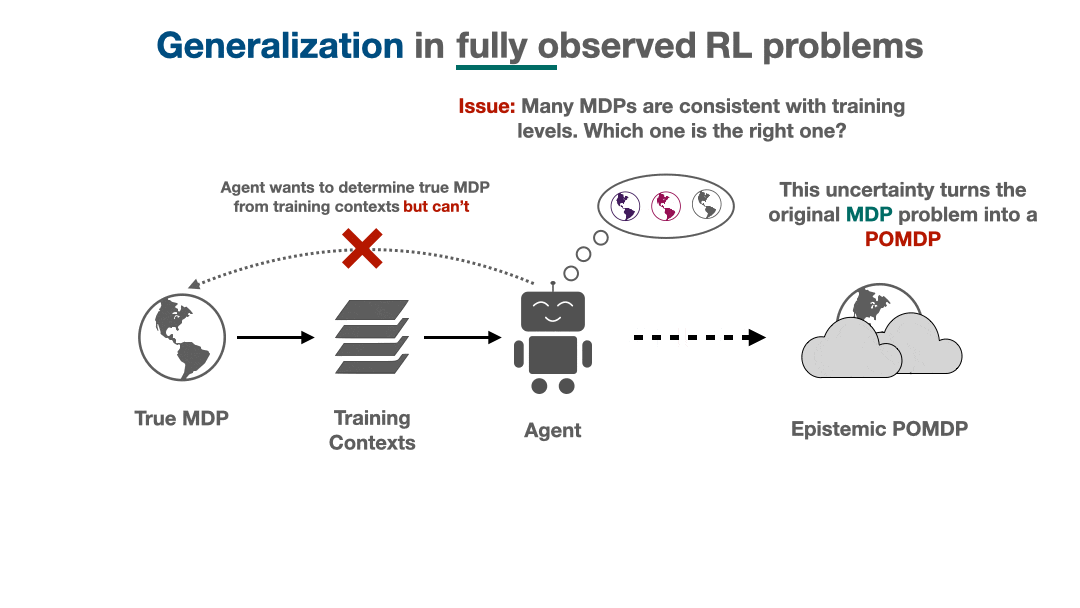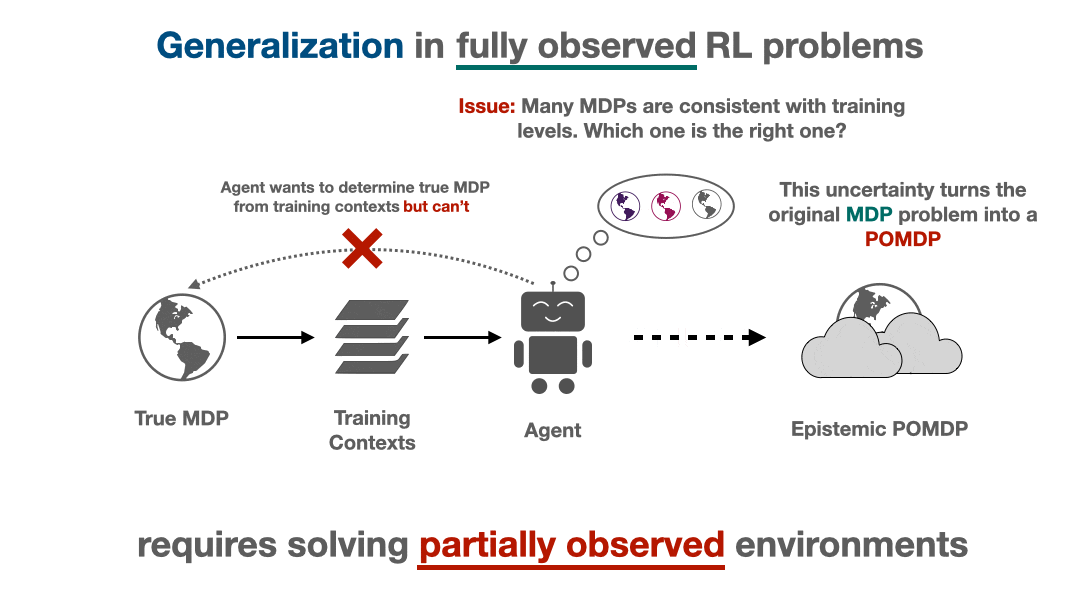
Actively steering towards regions of low uncertainty or taking information-gathering actions are two of a multitude of avenues an RL agent has to handle its epistemic uncertainty. Two important questions remain unanswered: is there a “best” way to tackle uncertainty? If so, how can we describe it? From the Bayesian perspective, it turns out there is an optimal solution: generalizing optimally requires us to solve a partially observed MDP (POMDP) that is implicitly created from the agent’s epistemic uncertainty.
This POMDP, which we call the epistemic POMDP, works as follows. Recall that because the agent has only seen a limited training set, there are many possible environments that are consistent with the training contexts provided. The set of consistent environments can be encoded by a Bayesian posterior over environments $P(M \mid D)$. Each episode in the epistemic POMDP, an agent is dropped into one of these “consistent” environments $M \sim P(M \mid D)$, and asked to maximize return within it, but with the following important detail: the agent is not told which environment $M$ it was placed in.
This system corresponds to a POMDP (partially observed MDP), since the relevant information needed to act is only partially observable to the agent: although the state $s$ within the environment is observed, the identity of the environment $M$ that is generating these states is hidden from the agent. The epistemic POMDP provides an instantiation of the generalization problem into the Bayesian RL framework (see survey here), which more generally studies optimal behavior under distributions over MDPs.
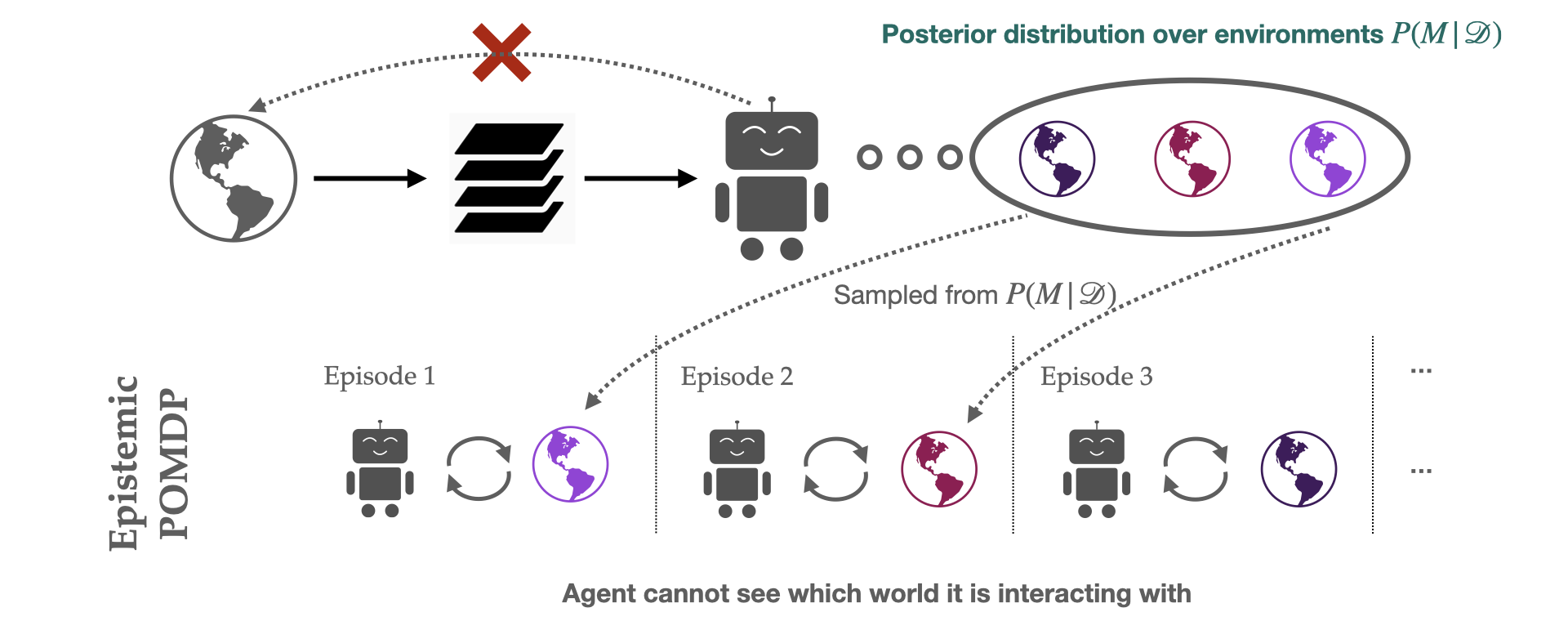
Let's walk through an example of what the epistemic POMDP looks like. For the guessing game, the agent is uncertain about exactly how images are labelled, so each possible environment $M \sim P(M \mid D)$ corresponds to a different image labeller that is consistent with the training dataset: $f\_M: X \to Y$. In the epistemic POMDP for the guessing game, each episode, an image $x$ and labeller $f\_M$ are chosen at random, and the agent required to output the label that is assigned by the sampled classifier $y = f\_M(x)$. The agent cannot do this directly, because the identity of the classifier $f\_M$ is not provided to the agent, only the image $x$. If all the labellers $f_M$ in the posterior agree on the label for a certain image, the agent can just output this label (no partial observability). However, if different classifiers assign different labels, the agent must use a strategy that works well on average, regardless of which of the labellers was used to label the data (for example, by adaptive process-of-elimination guessing or randomized guessing).
What makes the epistemic POMDP particularly exciting is the following equivalence:
An RL agent is Bayes-optimal for generalization if and only if it maximizes expected return in the corresponding epistemic POMDP. More generally, the performance of an agent in the epistemic POMDP dictates how well it is expected to generalize at evaluation time.
That generalization performance is dictated by performance in the epistemic POMDP hints at a few lessons for bridging the gap between the “optimal” way to generalize in RL and current practices. For example, it is relatively well-known that the optimal policy in a POMDP is generally non-Markovian (adaptive based on history), and may take information-gathering actions to reduce the degree of partial observability. This means that to generalize optimally, we are likely to need adaptive information-gathering behaviors instead of the static Markovian policies that are usually trained.
The epistemic POMDP also highlights the perils of our predominant approach to learning policies from a limited training set of contexts: running a fully-observable RL algorithm on the training set. These algorithms model the environment as an MDP and learn MDP-optimal strategies, which are deterministic and Markov. These policies do not account for partial observability, and therefore tend to generalize poorly (for example, in the guessing game and maze tasks). This indicates a mismatch between the MDP-based training objectives that are standard in modern algorithms and the epistemic POMDP training objective that actually dictates how well the learned policy generalizes.
Moving Forward with Generalization in RL¶
The implicit presence of partial observability at test time may explain why standard RL algorithms, which optimize fully-observed MDP objectives, fail to generalize. What should we do instead to learn RL policies that generalize better? The epistemic POMDP provides a prescriptive solution: when the agent’s posterior distribution over environments can be calculated, then constructing the epistemic POMDP and running a POMDP-solving algorithm on it will yield policies that generalize Bayes-optimally.
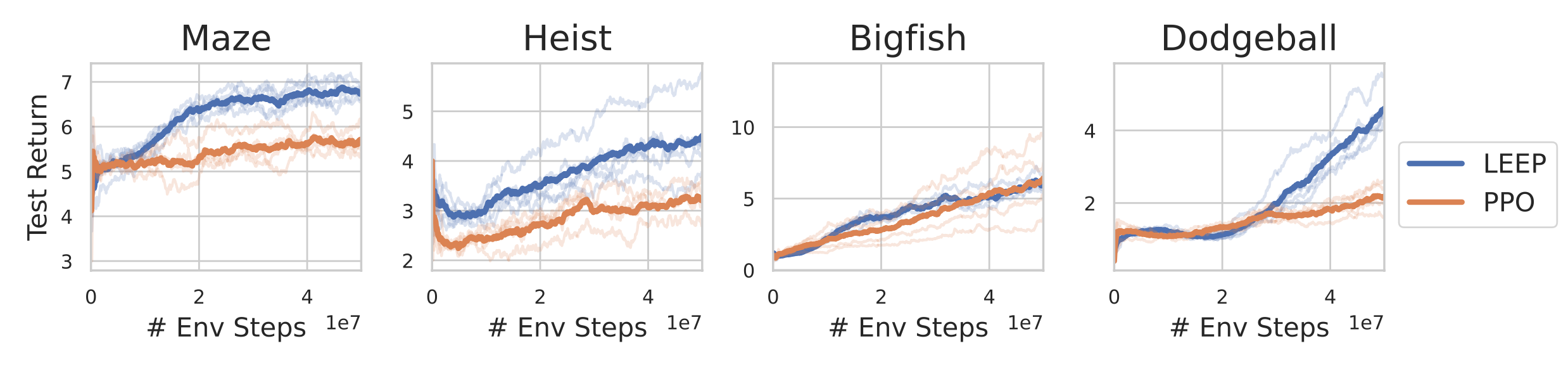
Unfortunately, in most interesting problems, this cannot be exactly done. Nonetheless, the epistemic POMDP can serve as a lodestar for designing RL algorithms that generalize better. As a first step, in our NeurIPS 2021 paper, we introduce an algorithm called LEEP, which uses statistical bootstrapping to learn a policy in an approximation of the epistemic POMDP. On Procgen, a challenging generalization benchmark for RL agents, LEEP improves significantly in test-time performance over PPO (Figure 3). While only a crude approximation, LEEP provides some indication that attempting to learn a policy in the epistemic POMDP can be a fruitful avenue for developing more generalizable RL algorithms.
If you take one lesson from this blog post...¶
In supervised learning, optimizing for performance on the training set translates to good generalization performance, and it is tempting to suppose that generalization in RL can be solved in the same manner. This is surprisingly not true; limited training data in RL introduces implicit partial observability into an otherwise fully-observable problem. This implicit partial observability, as formalized by the epistemic POMDP, means that generalizing well in RL necessitates adaptive or stochastic behaviors, hallmarks of POMDP problems.
Ultimately, this highlights the incompatibility that afflicts generalization of our deep RL algorithms: with limited training data, our MDP-based RL objectives are misaligned with the implicit POMDP objective that ultimately dictates generalization performance.
*This post is based on [the paper](https://arxiv.org/abs/2107.06277) “Why Generalization in RL is Difficult: Epistemic POMDPs and Implicit Partial Observability,” which is joint work with Jad Rahme (equal contribution), Aviral Kumar, Amy Zhang, Ryan P. Adams, and Sergey Levine. Thanks to Sergey Levine and Katie Kang for helpful feedback on the blog post.*